北京中考数学，为何中学老师感觉卷子难，但是小奥老师感觉卷子妙？

2019年的中考已经尘埃落定，而今年反响最为强烈的科目就是数学，普遍认为数学题难且新，不出意外，此次中考数学将成为拉分之王。我在看试卷的时候也为孩子们捏了一把汗，按说要难大家都难，但就怕心理不够强大的同学会崩溃导致影响发挥。看过今年中考试卷后，我觉得可以用八个字概括：“新而不偏，难而不繁。”今年的试卷更重视从思维和理解的层次来进行考察，这就使得很多只是死背结论、刷题不求甚解的同学遭了罪。

看完试卷后，我与很多数学老师交流过，发现了一个现象，中学老师普遍认为卷子出的难，但是小奥老师普遍认为卷子出的妙。身为既教小奥、又教中考的老师，这两种想法我都能理解。中学老师觉得难，主要是因为题目没有按套路出牌，平时总结的模型、题型能用上的不多，对于数学能力弱的孩子杀伤力很强；小奥老师觉得妙是因为今年的试卷侧重考查学生的思维和探究能力，以及对数学概念本质的理解，这更像是小学奥数，题目灵活多样，无章可循，但若能独立思考、举一反三，则一通百通。

接下来，我要结合今年中考典型题目，来分析中考传达的信息，以及给予我们学习上的启示。想查看中考试卷和答案可以点击左下角的“阅读原文”。

1、选择题的最后两道：

第7题的考察形式比较新颖，条件A、B、C知二推一，问有几个正确的命题。在课上教学时，我喜欢翻来覆去的带着同学们思考问题：条件和结论互换，命题是否成立。而且我从不告诉学生答案，而是让认为正确的学生找到证明方法，认为错误的同学举一个反例。这就是在教给同学们判断命题正误的方法，有的同学很喜欢探索，也有的同学不喜欢思考。这道题就能区分出这两类同学，平时不爱思考的同学，这道题只能束手无策。在初一刚学了不等式的时候，我就在班上带着学生讨论过：两个数的大小和它们倒数的大小关系，而且让学生自己利用不等式的性质来证明。结论是同号两数的大小关系与倒数大小关系相反，异号两数大小关系与倒数相同。在第7题的三个命题中，其中两个都可以由不等式的性质直接得到，而知道a、b的大小关系和a、b倒数的大小关系反推a、b符号是否相同，可以用反证法。假设a、b异号，由a>b得a正b负，与倒数关系矛盾，又因为a、b都不为0，所以a、b同号。平时没有养成思考的习惯，到了考场上现想是肯定行不通的。

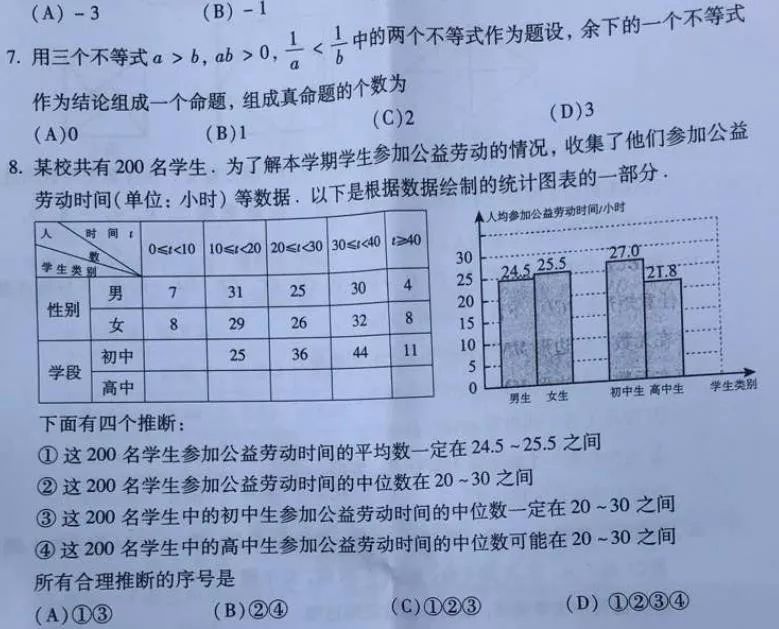
第8题在知道平均数和中位数的算法的基础上，还需要会估算，这是小奥的思想。①所有人的平均数一定介于男生平均数和女生平均数之间，这和两杯不同浓度的溶液混合，浓度必然介于二者之间是一个道理。②要判断中位数在那一段中，只需要知道总数和两头人数即可，在小奥中也有估算排名的题目，属于间接法。③是极端分析，在初中1~10这一段未知的情况下判断中位数落在哪个范围，初中明显在后两段人数较多2019北京中考数学试卷，那么只要看第一段人数为0时，中位数是否仍然在20~30之间即可。④仍然是极端分析，但是需要利用表中数据填出高中各段人数，这很像小奥中的比例计算与列表分析，见过这类题的同学应该不会慌。所以在这道题上，没学过小奥的同学是很吃亏的。

2、填空题：

第12题：看到这道题，小奥老师都笑了，小奥原题！方法是两条1×2的对角线和一条1×3的对角线可以拼成一个等腰直角三角形。

第16题：这道题考察的是同学们探究的能力，课上不太可能讨论过这个问题，但是会涉及到类似的情况。可以利用平行四边形的中心对称性，过矩形对角线交点并与矩形的边交于端点的线段必被中心平分，所以连接两条这样的线段的四个端点一定是平行四边形。若想进一步成为矩形，只需要这两条过中点的线段长度相等即可，所以以矩形中心为圆心画圆跟矩形四边相交即可，但是一定能做到吗？一定能，小奥里面讲过图形间的交点计数，圆与矩形最多可以有8个交点，以中心为圆心，只要半径大于矩形长的一半，且小于矩形对角线的一半即可。若想变为菱形，只需要这两条过中点的线段互相垂直即可，这样肯定能与矩形四边相交而且能画无数个。正方形是不行的，一个瘦长的矩形四边各取一点连一个正方形都画不出来。

3、解答题：

第22题：这道题出法比较新颖，是一道需要同学们自己画图的证明题，有点类似于选择第5题，主要考察弧、弦、圆周角之间的关系，同时如果能应用垂径定理逆定理，就可以快速找到圆的直径就是BC，从而得到DE是圆的切线。

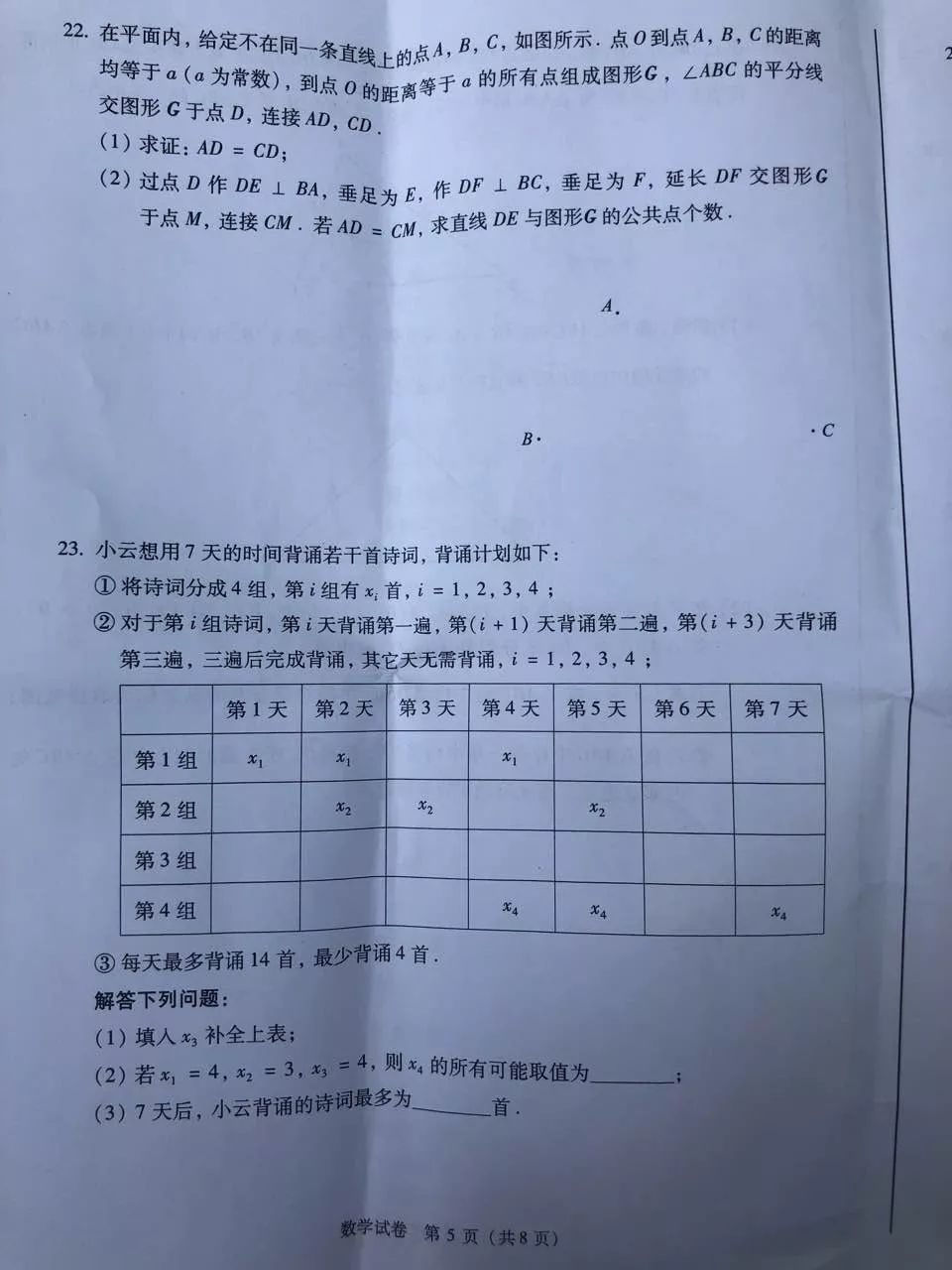
第23题：说这是一道小学奥数题也不为过，因为我把这道题拿到6年级的班上，很多同学可以做对，但是如果没学过奥数，这道题真的不好做，因为这道题太需要奥数思想了。首先是找突破口，有点像数字谜的思想，这道题最后一问的突破口是第4天，x1+x3+x4≤14，所以要想让总数最多，只要让x2最大就可以了。第2天x2+x1≤14，第3天x2+x3≤14，第5天x2+x4≤14，也就是说x2的最大值取决于另外三组最大的那个数，所以只要让x1、x3、x4中最大的那个数尽量小就行了，典型的小学奥数最值思想：最大数的最小值。由于x1+x3+x4=14，所以4、5、5即可满足，x2为9，故最多是23首。

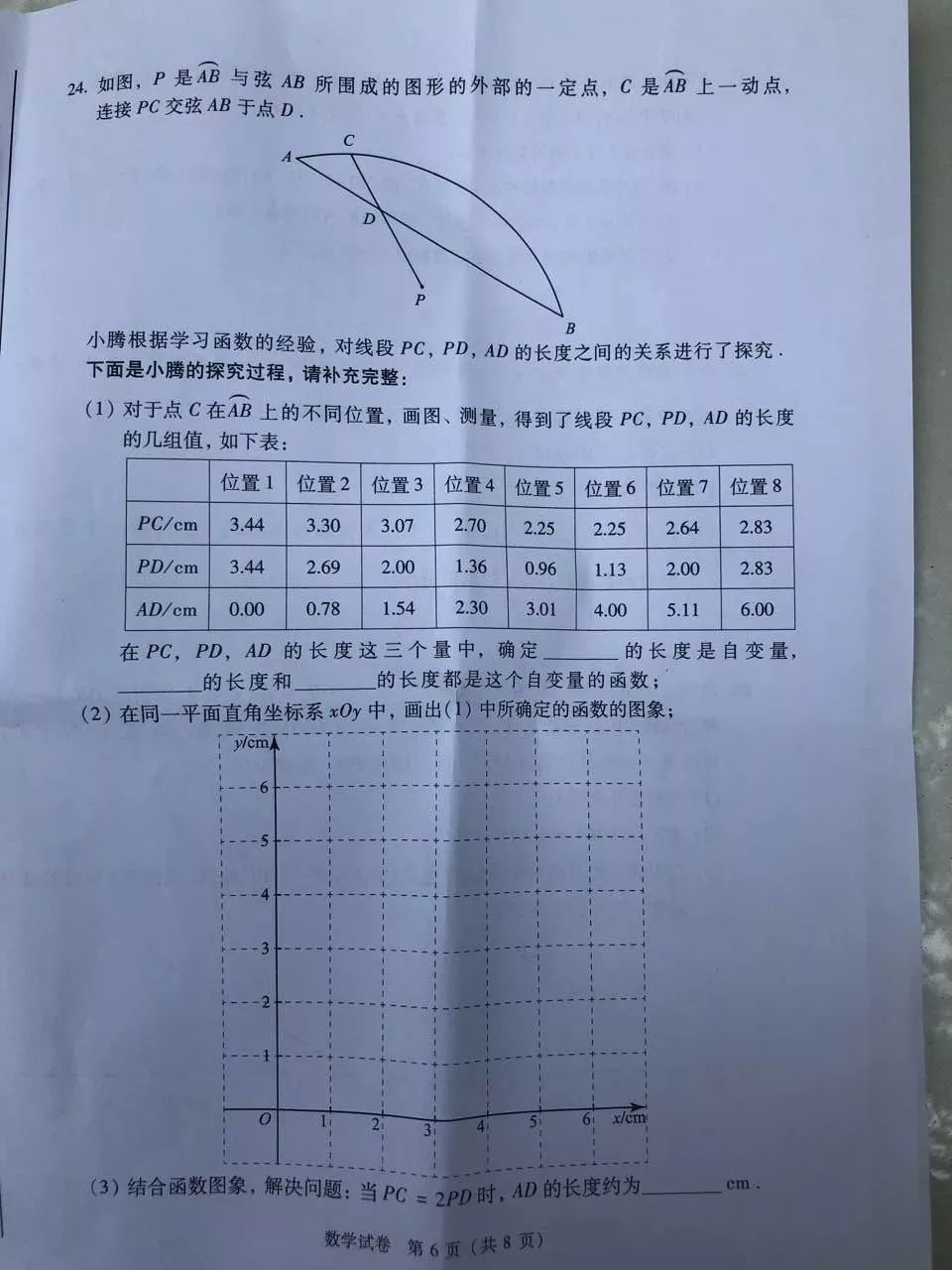
第24题：这道题是最坑但也是最妙的一道题，说它坑是因为要是第一问找不对自变量，后面都没分，说它妙是因为它考察了函数中最重要的东西——函数的定义。在课上，我一直强调，如果你连函数的定义都说不出来2019北京中考数学试卷，那说明你根本不懂函数！这句话果然在这次中考中印证了。我在课上还会用“欢乐抄10遍”的环节督促学生记住定义：对于每一个自变量，都有唯一的因变量与之对应，这才是函数关系。就好比一个爸爸可以有多个孩子，但是一个孩子只能有一个亲爹！分不清谁是儿子，谁是爹，扣分一点都不冤！在这道题里，从数据的表格中就能看出来只有AD可以作自变量。函数的概念如果不清晰，到了高中学曲线方程，更容易混淆。所以在这里栽个跟头，如果能记一辈子，其实不亏。

4、最后4道压轴题：

第25题：做这道题，你首先要知道一次函数斜率和截距对直线的影响：截距为1，说明直线过（0,1）；斜率绝对值越大，直线越抖，反之直线越平。由此画图就可以判断出，k>0时三角形内肯定有原点，故而考虑k＜0的情况，-1≤k＜0是可以的，但是随着斜率绝对值继续增加，直线y=kx+1一定在（-1,2）上方，只有当k为-2时，才能让这个整点落于底边上，此时内部无整点。但我认为这道题出的是败笔，因为如果再往下想，k为其它负整数时会不会有这种情况呢？可以证明是没有的，只要说明当k=n（n为小于-2的负整数）时，点（n+1，-n+1）一定在直线y=kx+1下方即可，但是需要计算，在中考有限的时间内，是不太可能想清楚的，虽说是直接写出答案，结论凭感觉这种事还是不太好。

第26题：这道题的原理有点像解决一元二次方程根分布问题2019北京中考数学试卷，利用的是两个连续函数图像若两端一高一低，则中间一定会有交点。对于这道题，要想让抛物线与线段有交点，只需要线段一头比抛物线低，另一头比抛物线高即可，利用这个关系列出不等式求解。很明显，a>0时两点都在抛物线上方，所以只讨论a时即可。如果做过类似题目并学会方法的同学，这道题是毫无难度的，但做题量少的同学若没见过这个类型，就没有办法了。

第27题：这道题是本次考试最难的一道题，难点在于如何找到OP的长度，很多解答直接给出OP=2，然后开始证明，如果是这样，这道题难度就大打折扣了。我用了一种构造方法可以求出OP：

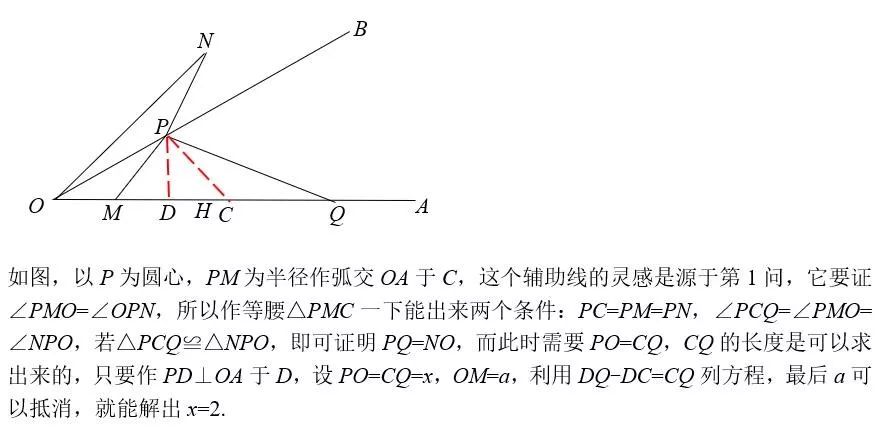
第28题：这道题考察的是圆与直线位置关系，题目比较灵活，需要具备一定的空间想象能力，题目中还涉及到了中位线、平行和相似。以DE为分界，分圆心在DE下方和圆心不在DE下方两类：第一类中E为切点时是临界点，此时的圆心及其下方都是可以的；第二类比较简单，圆心越低，弧越低，圆心越高弧越高，圆与底边相切时为临界点，此时的圆心及其上方都是可以的。第三问则需要在临界情况算出t，利用中位线和平行线间的比例计算更容易。这道题的前2问还是比较简单的，只是很多同学根本没有时间做到这里，所以如果合理安排时间，果断放弃思考27题而先做28题，分数可能会更高些。

总结：这套卷子有难度，前面有很多题目渗透了小奥思想，后四道压轴题每一道都不水，虽然计算量不大，但是需要想的地方很多，全面考察了思维能力而非生搬硬套。所以，可以理解很多同学对此次中考有怨念，但是更应该思考的是，我们需要在哪些方面注意：

首先要勤于思考，不能满足于知道结论，还要明白是怎么来的，并且要翻来覆去的想，如果条件能推出结论，那结论能不能推出条件，平时不去想，考试的时候就没时间想了。对于小学的同学来说，虽然现在点招的机会不多，但是奥数真的能锻炼思维，让你在数学中考中占据优势。

其次，基本概念，尤其是重要的概念必须记忆并理解，决不能犯懒，否则你很可能在中考中失去一道大题。

最后，在刷题时遇到难题，不能满足于看懂答案，而要多想想，这个答案是怎么想到的，你下次碰到能不能想出来。想办法找到思路的来源，把它总结成模型，这才是真正学会了这道题，否则刷题就是狗熊掰棒子。