【教师注意】数学好玩的趣味情境创设：个体兴趣养成的视角

【编者按】无论孔子的“知之者不如好之者，好之者不如乐之者”，还是毕达哥拉斯学派倡导好奇心为根源的“爱智慧”，都指向乐于学习的教育目标。本研究旨在从教师注意视角，通过案例研究，分析如何构建趣味情境，营造兴致盎然的轻松数学教育环境，让孩子在“玩”数学中，将情境兴趣转化成个体兴趣。

1. 研究背景

孔子在《论语•雍也》中指出，“知之者不如好之者，好之者不如乐之者”。毕达哥拉斯学派将认识万物之学定义为“爱智慧”，是激发好奇心，以惊异为根源的精神的生殖力和创造力。但现实中枯燥乏味的数学课堂比比皆是，数学面目可憎，学生兴趣索然; 家长辅导孩子数学甚至达到了“剑拔弩张”之情状。如何营造兴致盎然的轻松数学教育环境，似乎成为一个颇具挑战的社会性话题。

王灿明（2020）研究“李吉林情境教育思想”时指出，对情境教育的不懈探索，让李吉林越来越重视情感的作用。一开始趣味数学24点100题，她将情感作为情境教学的“动因”，后来又将它看成情境教学的“纽带”，最后将它视为情境教育理论的“命脉”。因而，以调动学生情绪为中心，激发学生兴趣，成为教学情境设置的关键，因而趣味情境设置成为本研究中心话题。

2. 理论架构

2.1情境兴趣与个体兴趣

什么是兴趣？赫尔巴特将学习兴趣定义为主动性，它与漠不关心相反，是个体在教育中所表现出来的一种欲望冲动。

杜威认为兴趣“含有居间的事物的意思 ，即把两个本来远离的东西联结起来的东西”。“兴趣就是一个人和他的对象融为一体”，兴趣是儿童的需要与教学环境的营造。杜威进一步指出，如果我们能够发现一个儿童的急迫需要和能力，我们又能够提供一个有材料、有用具、有资料的环境——自然的、社会的和理智的——以指导它们恰当的运作，我们就不需要去考虑兴趣。

20世纪90年代初，美国学者海蒂（Hidi，S.）将兴趣分为个体兴趣（ ）和情境兴趣（ ）。个体兴趣类似于学生主体因素，一般指个人倾向或偏好，它以人的知识、价值观及积极感情为基础，具有相对稳定性和持久性。情境兴趣类似于教学环境因素，一般指学生被教学中的某些条件、刺激所吸引，如复杂性、新颖性、不确定性、冲突性等内容，但这种吸引往往不够稳定或持久。

海蒂认为，从情境兴趣到个体兴趣，大致要经历情境兴趣的激发、维持、个体兴趣的萌芽与成熟四个阶段。每一阶段各有其独特的特征、发展趋势以及促使兴趣由低阶段向高阶段转化的条件。

2.2 学习兴趣与教育相互作用的现象学原理

现象学所研究的既不是单纯的主体，也不是单纯的客体，而是在主体向客体投射的意向性活动中，主体与客体之间的相互关系以及其所构成的世界。

按照现象学观点，教育情境是焦点，兴趣是边缘域，两者之间相互作用过程也可以运用图1展现出来。

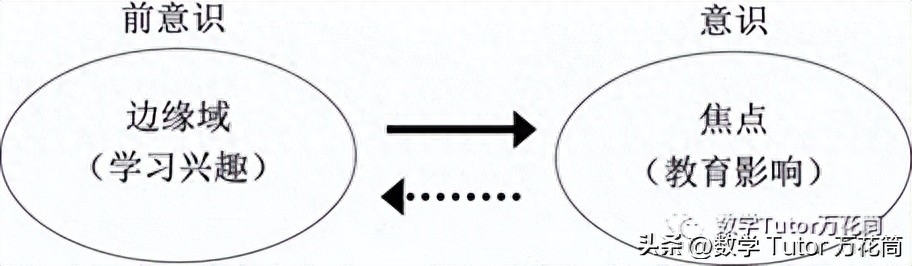
图1：边缘域与焦点关系示意图

从图1看出，教育影响对个体兴趣不能直接产生作用，需要个体能动加工，也就是被认知评价后，才能作用于边缘域以决定是否形成学习兴趣。决定学习兴趣的是主体对该教育影响的解读、评价或归因。它们之间是情绪建构理论的“激发事件—— 认知评价——情绪结果”关系。海蒂认为，“对事件的认知评价引起并建构了相应的情绪体验”，而学习中积极的情绪体验正代表着学习兴趣的可能。

3. 案例研究

，Paul（2001）研究显示，学生学习兴趣的养成有赖于激发学生产生“有趣”的体验，有赖于教育内容对学生来说是重要而有价值的，有赖于教师采取深入浅出或通俗易懂的教学策略，有赖于新旧知识之间的联系等。本研究从真实教学案例分析出发，探求影响趣味数学情境设置，激发学生个体兴趣的可能的教学因素。

标题：从课本到“数学疑云”：柯南再显身手

悬疑故事引入：（营造情境兴趣）

米花町在商店街举行“首次跑腿”少儿跑腿大赛，参与者们要独自按照清单上的商品逐一跑腿购买，最快购买完成并返回七点米花公园的小朋友获胜。……

柯南和小伙伴组成的少年侦探团作为记录者参与其中，追随步美家附近的小宏。可是在参赛过程中小宏却被什么人狙击，离奇失踪了。（激发好奇心，调动情绪）

柯南他们分头搜寻商店街终于在一个小路上发现了小宏的身影，正要追上去却被一辆货车拦住了去路，只有快速通过四道关卡才能移开货车追上小宏，他们能否成功帮助小宏脱险呢？

他们需要解决的关卡：

关卡1：找出“漏网之鱼”：班上有40个学生，学号分别是1、2、3、…、40。一次数学考试结束后，老师清点试卷时发现竟然只有39张卷子。如果不借助任何工具，仅通过依次查看每张卷子上写的学号，怎样才能找出没交卷的那位同学的学号？

柯南解法：学号和=1+2+3+...+40=820

减去看到的学号

820-学号-...-学号=?

剩下的数就是缺失的那个学号

巧用总和加、减法解决了难题！（全局观念激发学生兴趣）

关卡2：估算时间：周一早上8:00至9:00之间的某个时刻，爸爸从家出发去上班，此时手表上的时针和分针正好重合。下午2:00至3:00之间的某个时刻，爸爸回到家，此时手表上的时针和分针正好指向完全相反的方向。那么爸爸从出发到回家一共用了多少时间？

（下面的问1、2、3、4、5属于精巧性提问）

问1：分针走一圈需要60分钟，时针走一圈需要=720分钟，能算出分针、时针的速度吗？

时针速度=360°/720=1/2（度/分）

分针速度=360°/60=6（度/分）

爸爸出发的时刻：上午8:00至9:00之间的某个时刻，时针和分针重合。

问2：从8点开始，需要多少分钟，分针追上时针？

问3：分针比时针多走几度？8x30=240度

分针-时针重合所用时间为：240/(6-1/2)=480/11分钟（除法意义、行程问题意义）

所以爸爸出发时刻是8点480/11分

问4：从2点开始，需要多少分钟分针追上时针并与时针反向？

问5：分针比时针多走几度？

2x30+180=240度

分针时针反向状态所用时间为：240/(6-1/2)=480/11分钟

所以爸爸回家时刻是14点480/11分

总之，爸爸出发时刻：8点480/11分 爸爸回家时刻：14点480/11分

从出发到回家一共用了：14点480/11分-8点480/11分=6小时（运用真实时钟图片，与学生生活场景联系，建立新旧知识关联）

关卡3：服药难题

奶奶每天要同时服用外观一样的A、B两种药片各一粒。一天，奶奶不小心多倒出了一粒B药片。现在她手心上一共有三粒药片，并且她无法区别哪个是A，哪个是B。请问如何才能严格遵循药方服用药片趣味数学24点100题，并且不能有任何的浪费？

再取出一粒药片A放在手心

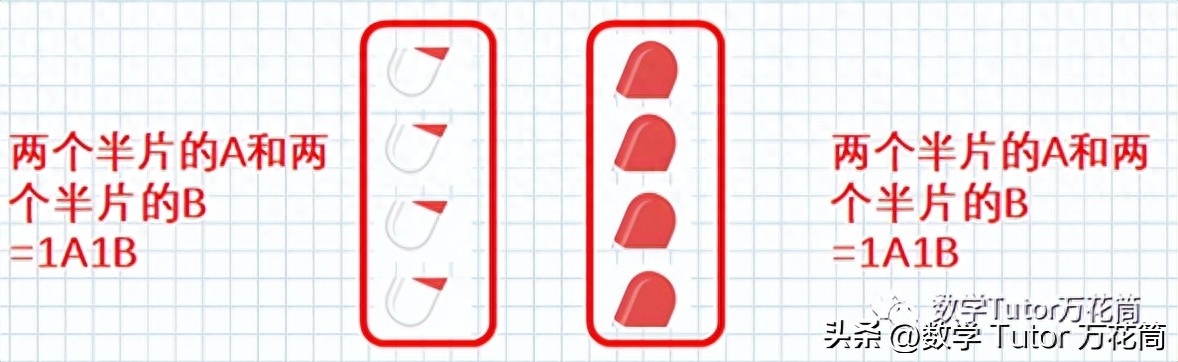
（全局观念激发兴趣，生动图片展示真实尊老爱幼生活场景，帮助奶奶解决难题，获得个人成就感体验）

关卡4：切割游戏

一个长方形蛋糕被切去1个角，还剩几个角？

讨论：

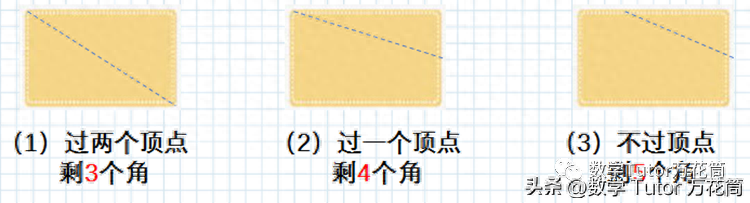
蛋糕角越切越多！（用认知疑惑激发个体兴趣萌芽）

故事结尾：柯南成功通过4个关卡，顺利帮助小宏脱险啦！（前后呼应，维持情境兴趣）

4. 教学建议

兴趣犹如“一双看不见的手”，通常居于言说的幕后进行着操作。那么，怎样的“巧手”才能有利于促进学生的个体兴趣的养成呢？

4.1 尽可能建构有丰富个体体验与评价的教学活动

兴趣养成需要经历情境兴趣的激发、维持、个体兴趣萌芽、成熟等四个阶段。从情境兴趣转化为个体兴趣，特别需要个体能动参与。教师应尽可能建构个体参与感、体验感强的教学活动，扭转学生对数学枯燥无味的看法，乐于“玩”数学。

4.2 用精巧性提问创设趣味情境

认识到情境兴趣与个体兴趣的差异趣味数学24点100题，教师注意的关键是挖掘学生好奇心，调动学生能动性。平时注重搜集饶有趣味的数学实际问题，并尽可能精巧设计提问，拉近学生生活，启发思维，从畏惧数学思维的泥潭中走出来，使得“做数学”变得津津有味。

4.3 注重情境与知识的转化

情境与知识的转化有利于学生自我评价，是形成个体兴趣的关键。情境-知识转化首先以数学概念为基础，是建立在对概念理解的意义之上。比如本案例研究中关卡2的行程问题、除法的意义。更重要的是体现全局观价值，站在全局视角看待问题。比如本案例研究中关卡1、3都蕴含全局观念。不拘泥于细节，从整体出发解决问题，给人豁然开朗感觉的整体观，让学生体验驾驭感、成就感。